How to Sort By Walking on a Tree
Daniel Graf, ETH Zurich, grafdan@ethz.ch
Implementation of the sorting algorithm presented in the paper presented at ESA 2015.
This project is part of my Master Thesis titled "Scheduling and Sorting Algorithms for Robotic Warehousing Systems" that I worked on from January to July 2015 at ETH Zürich.
Here are two Lego stop motion animations that show the sorting algorithm in action and how an optimal scheduling of the robot can minimize customer waiting time.

The command line visualization of the sorting algorithm looks like this:
This page contains the implementation of the algorithms presented in Theorem 1 and Theorem 3 of the paper. They can find shortest sorting walks on paths and on trees. The final walk can be visualized for demonstration purposes. The code also checks the length of the sorting walk against the lower bound given in Theorem 2.
Usage Tutorial
Let me walk you through the first steps with the code. If anything along the way is unclear, please let me know.
Download and Compile
The code is written in C++11. It does not require any additional libraries or dependencies, except for the standard template library.
Please start by downloading the source code here: Source Code (40KB)
Store the file as treesort.cpp in a local directory. Then compile it with the shell command g++ treesort.cpp -o treesort -std=c++11 (requires a recent GNU C++ compiler installed).
You can run the binary by typing ./treesort into your shell.
Getting Started
When started, the program shows an interactive run loop. Type a command and press enter to generate a new warehouse or to change its state.
./treesort $> type your command here
If you press h and enter you will get a list of all available commands.
==================== || Tree Sort Help || ==================== Generate or load a problem -------------------------- l/load [filename] Load a tree from a file. rp/randompath [n] Generate a path of n boxes with a random permutation. rt/randomtree [n] Generate a tree of n boxes with a random permutation. Solve a problem -------------------------- s/step [p] [b] Perform a single sorting step to vertex p with box b. x/solve Solve the problem and print a shortest sorting walk. v/verify Verify that the sorting walk is valid and as short as the theorem claims it to be. a/animate Animate the sorting walk of the robot in ASCII. t/test Generate random paths and trees and check their solutions for validity and optimality. Utilities -------------------------- d/debug Toggle debug output when solving a problem (prints the contraction hierarchy and its DMSTs). e/speed [v] Set the animation speed. Default is 20. p/print Print the current state of the warehouse.
Creating a Graph and a Permutation
Before we can start sorting boxes, we first need to have the graph G and the permutation P that represent the initial state of the warehouse. The fastest way to get started is to generate a random path or a random tree.
$> randompath 7
$> print
Pi: (1) (2 6 3) (4 7) (5)
Graph:
1 2 3 4 5 6 7
[1] [6] [2] [7] [5] [3] [4]
\_/
$> randomtree 7
$> print
Pi: (1 6 7) (2 3 5) (4)
Graph:
1 [6]
/ \\_/
-- ---
/ \
2 [3] 3 [5]
/ \ |
| \ |
/ \ |
4 [4] 7 [1] 5 [2]
|
|
|
6 [7]
$>
We used the print command to get a text rendering of the generated state. It shows the permutation of the boxes in cycle notation as well as the graph with the position of the robot (symbolized by the characters \_/) and the location of all the boxes (sybolized by the characters [?]).
Alternatively, we can load a specific configuration from a text file. Such a file has to contain three lines which have to describe a tree on n vertices, rooted at vertex 1. The first line has to contain n, the number of nodes in the graph. The next line has to contain (n-1) integers, the i-th of them being the index of the parent node of node i+1. Finally, the third line has to contain n integers, representing the initial permutation of the boxes. As an example, the tree shown in the image below, can be represented with this file:
8 1 1 2 2 3 6 6 4 2 7 1 3 8 5 6
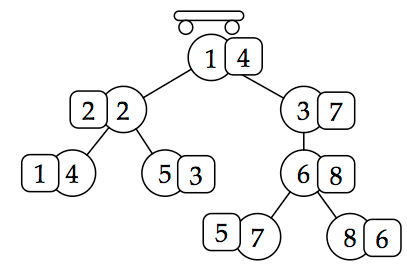
Just store this file in the same directory as the treesort binary and then load it like this:
$> load example.txt
Read problem of size: 8
$> print
Pi: (1 4) (2) (3 7 5) (6 8)
Graph:
1 [4]
/ \\_/
-- ---
/ \
2 [2] 3 [7]
/ \ |
| \ |
/ \ |
4 [1] 5 [3] 6 [8]
/ \
| \
/ \
7 [5] 8 [6]
Solving Sorting Problems
Applying Single Steps
You can apply individual sorting steps with the step command. This takes two arguments: the vertex index that the robot should move to and the box index that it should carry along. Use 0 as box index, if the robot should move without a box. Invalid steps are ignored.
$> print
Pi: (1 4) (2) (3 7 5) (6 8)
Graph:
1 [4]
/ \\_/
-- ---
/ \
2 [2] 3 [7]
/ \ |
| \ |
/ \ |
4 [1] 5 [3] 6 [8]
/ \
| \
/ \
7 [5] 8 [6]
$> step 2 4
Pi: (1 4) (2) (3 7 5) (6 8)
Graph:
1 [_]
/ \
-- ---
/ \
2 [2] 3 [7]
/ \\4/ |
| \ |
/ \ |
4 [1] 5 [3] 6 [8]
/ \
| \
/ \
7 [5] 8 [6]
$> step 4 4
Pi: (1 4) (2) (3 7 5) (6 8)
Graph:
1 [_]
/ \
-- ---
/ \
2 [2] 3 [7]
/ \ |
| \ |
/ \ |
4 [1] 5 [3] 6 [8]
\4/ / \
| \
/ \
7 [5] 8 [6]
$> step 2 1
Pi: (1 4) (2) (3 7 5) (6 8)
Graph:
1 [_]
/ \
-- ---
/ \
2 [2] 3 [7]
/ \\1/ |
| \ |
/ \ |
4 [4] 5 [3] 6 [8]
/ \
| \
/ \
7 [5] 8 [6]
Finding and Printing the Shortest Sorting Walk
The solve command applies the algorithms of Theorem 1 (for paths) and Theorem 3 (for general trees) to find the shortest possible sorting walk and then prints all its steps.
$> solve Sorting Walk S: (2,4)(4,4)(2,1)(1,1)(3,1)(6,7)(8,8)(6,6)(7,7) (6,5)(3,5)(1,5)(2,5)(5,5)(2,3)(1,3)(3,3)(1,1)
Verify the Solution
The verify command simulates the sorting walk to ensure that it is valid, i.e. correctly sorts the input. It also compares its length to the bounds given by the tight lower bounds in Theorem 2.
$> verify Solution walk of length 18 -> this matches the bound of the theorem! -> it correctly sorts the input!
Animate the Solution
Finally, the animate command shows a text visualization of the sorting process by performing the steps of the solution one by one.
On a path
On a tree
Extra Commands
There are a few additional commands that are only useful for development purposes.
speed lets you set a different animation speed. Default is 20.
debug toggles the debug output when solving a problem. If activated, this prints all the intermediate steps of finding the directed minimal spanning tree.
test repeatedly generates small random paths and trees, solves and verifies them which is useful for finding small counterexamples for buggy implementations.
I am looking forward to hearing from you.